[最も選択された] 三 平方 の 定理 直角 三角形 319134-三平方の定理 直角三角形だけ

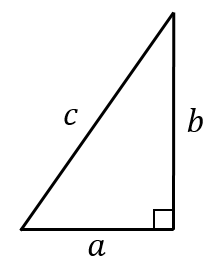
英 Pythagorean theorem ）は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} が成り立つという 等式 の形で述べられる 。 三平方の定理（ さんへいほうのていり ） 、 勾股弦の定理（ こうこげんのていり ） とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内2/9/ ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式：a² b² = c²46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2b^2=c^2 47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2b^2=c^2 ,那么这个三角形是直角三角形 86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应 线段成比例

かみのドリル 三平方の定理

三平方の定理 直角三角形だけ

三平方の定理 直角三角形だけ- 1、利用直角三角形中两锐角之和为90° 2、利用全等三角形 勾股定理的逆定理：如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形。 初中数学1 3、利用勾股定理的逆定理证明 4、利用等腰三角形"三线合一"证明直角三角形斜边中线定理逆命题 编辑 语音 其 逆命题 1：如果一个三角形一条边的中线等于这条边的一半，那么这个三角形是直角三角形，且这条边为直角三角形的斜边。 逆命题1是正确的。 以该条边的中点为圆心，以中线长为半径作圆，则该边成为圆的直径，该三角形的另一个顶点在 圆上 ，该顶角为 圆周角 。 因为直径上的圆周角是直角，所以逆命题1成立。 原命题

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

22/8/ 直角三角形边长公式 1351 文/董玉莹 应用勾股定理：斜边平方=两直角边平方之和。例如，对于任意一直角三角形而言，设两直角边长度分别为a和b，斜边长为c，则根据勾股定理可得到公式：a²b²=c²。19/2/21 直角三角形の定理（三平方の定理） 直角三角形では、辺の長さに関する 三平方の定理 が成り立ちます。 三平方の定理 直角三角形の直角を挟む 辺の長さを , とし、斜辺を とすると、 が成り立つ。 辺のうち任意の 辺の長さがわかれば、三平方の定理を使って残りの 辺の長さを求められますね。 なお、「三平方の定理」については以下の記事でより詳しく説明し次のような直角三角形の3辺の長さについては， a 2 b 2 =c 2 が成り立ちます．（これを 三平方の定理 といいます．）

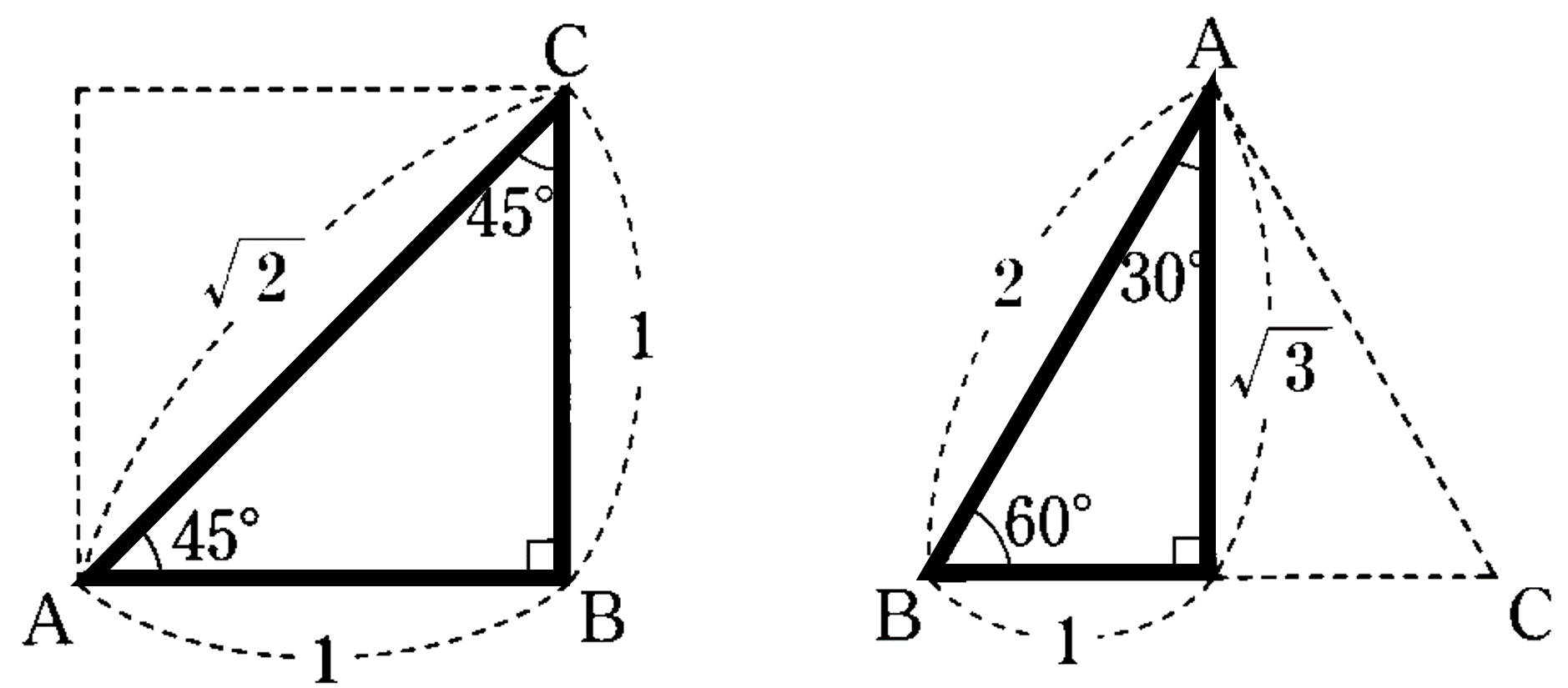
三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います 勾股定理1第十七章 勾股定理17．1 勾股定理第1课时 勾股定理2．(4分)已知一个直角三角形三边的平方和为1800，则斜边长为( )a．80 b．30 c．90 d．3．(4分)如图，一棵大树在离地面3米处折断，树的顶端落在离树干底部4米处，那么这棵树折断之前的高度是( )a．12米b．8米c．5米d．5或7米第十七章 勾股定理

13/6/21 補足：ピタゴラス数（整数の話題） 一般に，三つの自然数の組 ( a, b, c) (a,b,c) (a,b,c) が三平方の定理の式 a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たすとき， ( a, b, c) (a,b,c) (a,b,c) を ピタゴラス数 と呼びます。 有名なピタゴラス数として，直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ底辺と斜辺底辺と角度斜辺と高さ斜辺と角度高さと角度面積と底辺面積と高さ面積と斜辺面積と角度 6桁10三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理の証明と使い方

28/4/ 方法/步骤 1/4 分步阅读 第一：直角三角形边长公式：c²=a²b² ：已知三角形两条直角边的长度 ，可按公式c²=a²b²计算斜边。 2/4 第二：直角三角形边长关系： 1、两边之和大于第三边；2、直角三角形中两直角边的平方和等于斜边的平方 (c²=a²b²）。 3/4 第③利用三角形内角和定理求第三个角 例3在 ABC中，已知 ， ， ，求b及A 解析由题意得 ， ， 4、已知三边解三角形 已知三角形的三边a，b，c，解三角形的步骤： ①利用余弦定理求出一个角； ②由正弦定理及 求其他两个角 例4在 ABC中，已知 ， ， ，求最大角和 三角形三边关系定理及推论的作用 ①判断三条已知线段能否组成三角形； ②当已知两边时，可确定第三边的范围； ③证明线段不等关系。 特殊 直角三角形 性质1：直角三角形两直角边的平方和等于斜边的平方。 性质2：在直角三角形中，两个锐角互余。

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

無料 中３数学 基本解説 解答プリント 334 三平方の定理２ 比の利用

（4）重心到三角形三个顶点的距离平方和最小 （5）在直角坐标系中，重心的坐标是顶点坐标的算术平方根 （6）重心是三角形内到三边距离之积最大的点 角平分线：三角形的内心 （1）每一个三角形也有三条角平分线，这三条角平分线的交点叫做"内心"直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき 三平方の定理（ピタゴラスの定理）と公式の証明忍者が用いた三角の知恵｜アタリマエ！ 中3数学では、 三平方の定理（ピタゴラスの定理） を勉強してきたよな？ 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²＋ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。 今回はそのための基礎トレーニングだ。

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

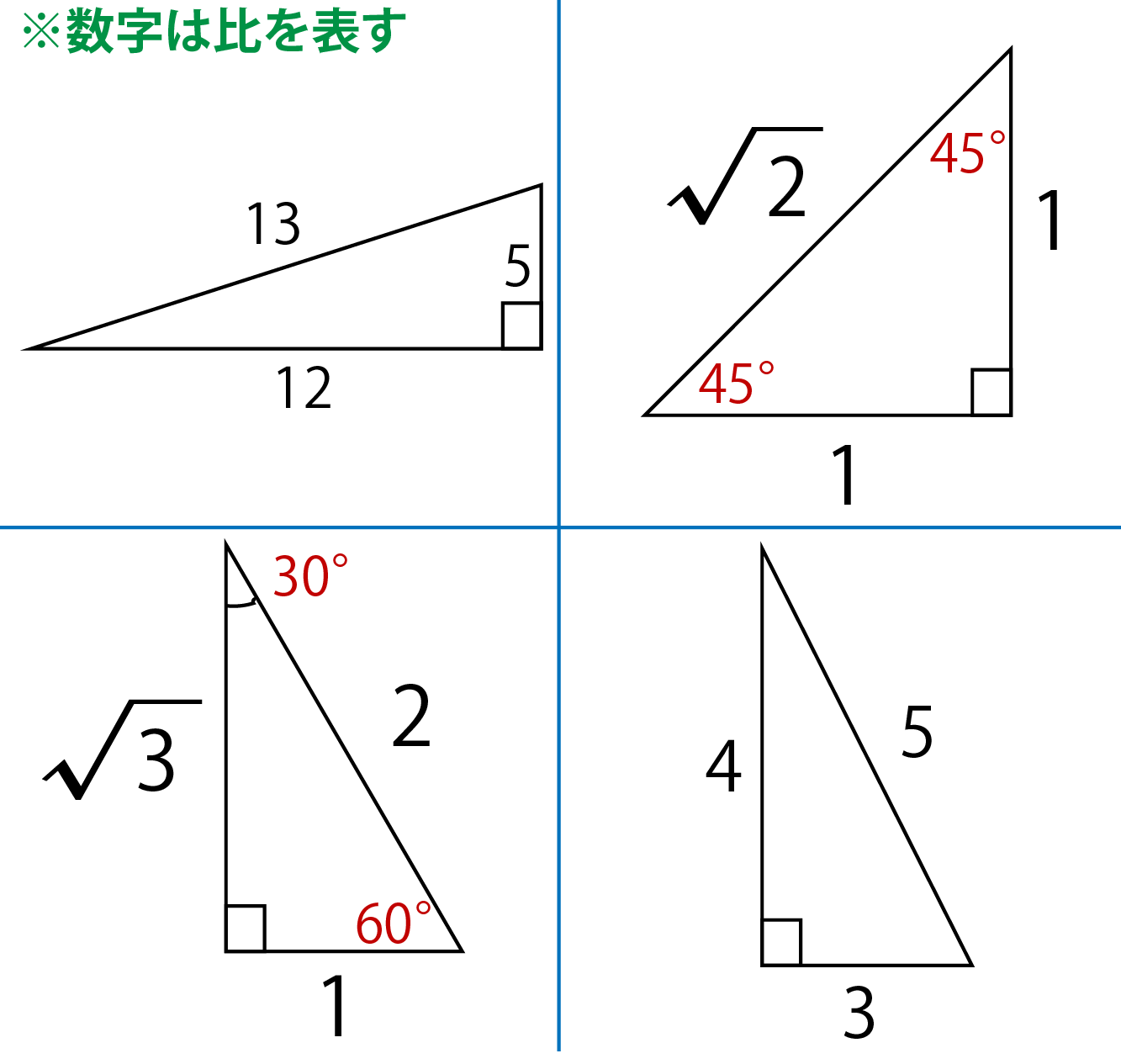
三平方の定理は直角三角形 c 2 の平方 根を見つけ 与えられた三角形を見ます。この時点で三つ全ての角の角度と辺aの長さが分かっています。そこで、これらの情報を正弦定理に代入して、残り二辺の長さを求めます。4/1/17 勾股定理的证明方法汇总一 做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形 从图上可以看到，这两个正方形的边长都是a b，所以面积相等 即a的平方加b的平方覚えるだけで簡単に三平方の定理の計算問題が解けるよ。 覚えると便利！直角三角形の3つの比 それじゃあ早速、中学数学の問題でよく出てくる、 直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

かみのドリル 三平方の定理

12/9/ 直角三角形的两条直角边的平方和等于斜边的平方（勾股定理）。 *勾股定理逆定理：如果三角形的三边长a，b，c满足a²b²=c²，那么这个三角形是直角三角形。 ③直角三角形斜边的中线等于斜边的一半。 ④三角形的三条角平分线交于一点，三条高线的所在三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、 ピタゴラスの定理 とも呼ばれます。 三平方の定理（ピタゴラスの定理） 3 辺の長さが a, b, c の直角三角形 上の直角三角形において21/8/07  直角三角形三边关系全部 132 三角形两边平方和与第三遍平方的关系断定三角形形状 2 三角形的三条边之间有什么关系 709

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

特別な直角三角形の３辺の比 の問題が分からないんですけど やり方を教えてく Clearnote

 三角形的边长公式 在任何一个三角形中，任意一边的平方等于另外两边的平方和减去这两边的2倍乘以它们夹角的余弦。 几何语言：在 ABC中，a²=b²c²2bc×cosA；此定理可以变形为：cosA=（b²c²a²）÷2bc。 c²=a²b² ：已知三角形两条直角边的长度 ，可按公式c²类似问题5：已知直角三角形的三边长为连续的整数,求这个三角形的三边长（列出一元二次方程的具体步骤数学科目 设最短边为x,因为是连续的整数所以另外两边为x1,x2 因为三角形是直角三角形,所以x2为斜边 利用勾股定理,得：x^2(x1)^2=(x2)^2 Pythagorean theorem は直角三角形の3辺の長さの関係を表す 斜辺の長さを c 他の2辺の長さを a b とすると定理は が成り立つという等式の形で述べられる 三平方の定理さんへいほうのていり勾股弦の定理こう

三平方の定理の証明と使い方

三平方の定理を直角三角形二つで証明 Youtube

在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半； （4）勾股定理：直角三角形两直角边的平方和等于斜边的平方； （5）逆定理：如果三角形的三边长满足两边的平方和等于第三条边的平方， 那么这个三角形是直角三角形； 直角三角形的性质： ①直角三角形的两个锐角互为余角； ②直角三角形斜边上的中线等于斜边的一半； ③直角三角形的两直角边的平方和等于斜边的平方（勾股定理）； ④直角三角形中30度 角所对的直角边等于斜边的一半； 46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2b^2=c^2 47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2b^2=c^2 ,那么这个三角形是直角三角形 48定理 四边形的内角和等于360° 49四边形的外角和等于360°

直角三角形の合同条件

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

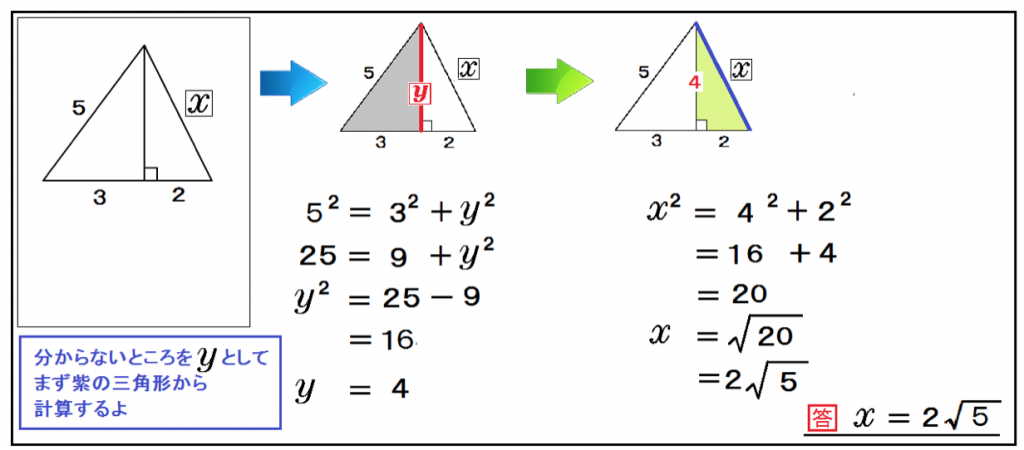
三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理 ピタゴラスの定理

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

感銘を受けた数学 三平方の定理の美しき証明たち 大人のための数学教室 和 Note

三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

特別な直角三角形の辺の比 無料で使える中学学習プリント

三平方の定理 覚えておきたい基本公式を解説 数スタ

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

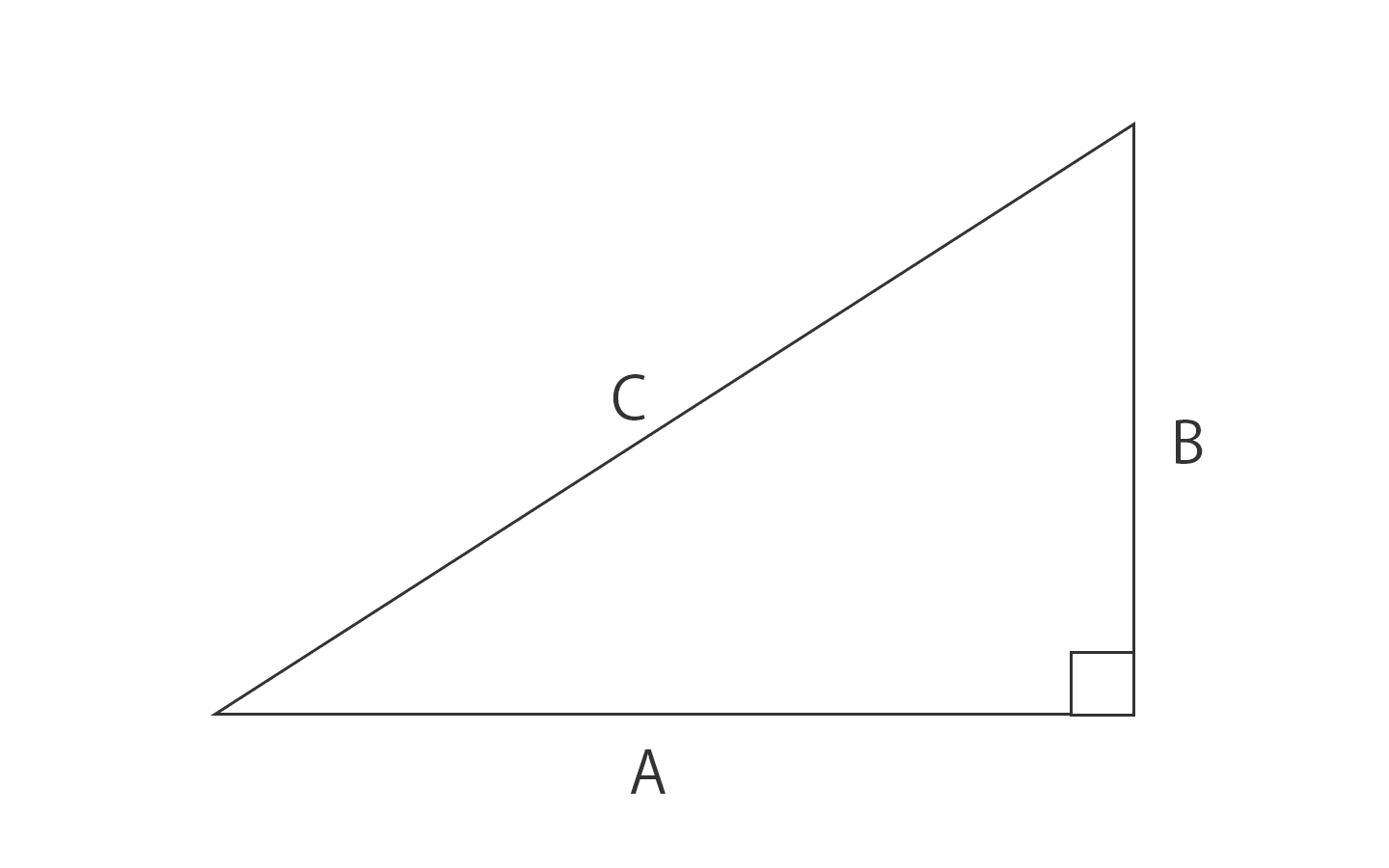
Python 三平方の定理 Unpyside

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

中学高校数学laf先生 質問回答中 Su Twitter 証明シリーズ 三平方の定理 直角三角形の斜辺の長さをc 残りの二辺の長さをそれぞれaとbとおくと C 2 A 2 B 2 なんで と思った人も多いかと思ったので 実際に証明してみました 理解できた人rt T

Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方の定理 自動計算サイト

三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

７章 三平方の定理 タカラゼミ

三平方の定理 おやじさん ネット

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理について考える５ 直角三角形の合同条件のひとつ 身勝手な主張

まる先生 サンドイッチの3辺は決まっている 三平方の定理 まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 高校入試 高校受験 まる練数学 三平方の定理 斜辺 直角三角形 T Co Pwwphgrjgq Twitter

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

質問にお答えします 小学生でもわかる数学とは 教育研究所arcs

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

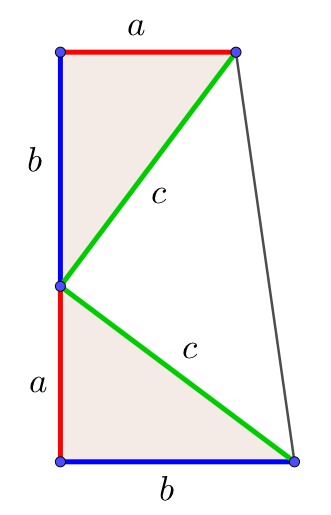
三平方の定理の証明３ 大統領の台形 キソカラ

余弦定理

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座

3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ

三平方の定理の逆ってなに どうやって証明するの 数スタ

直角三角形 Wikipedia

三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

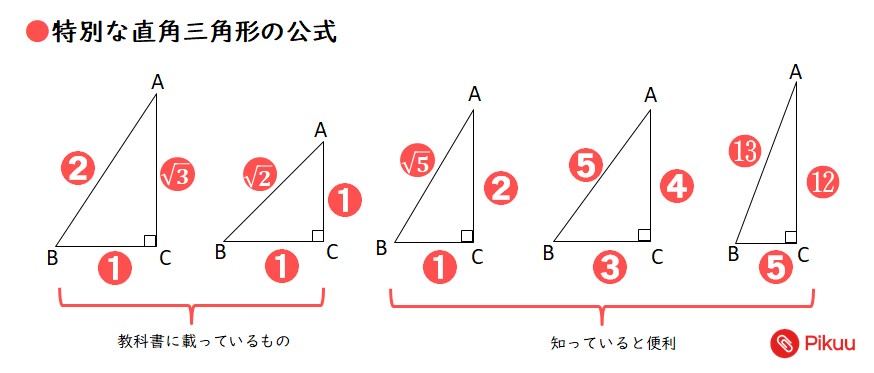
高校入試対策数学 特別な直角三角形を使った問題 Pikuu

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

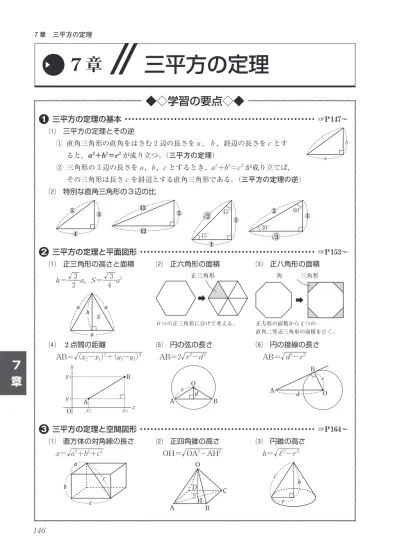
見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理を英語で読んでみる

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方の定理の証明と使い方

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

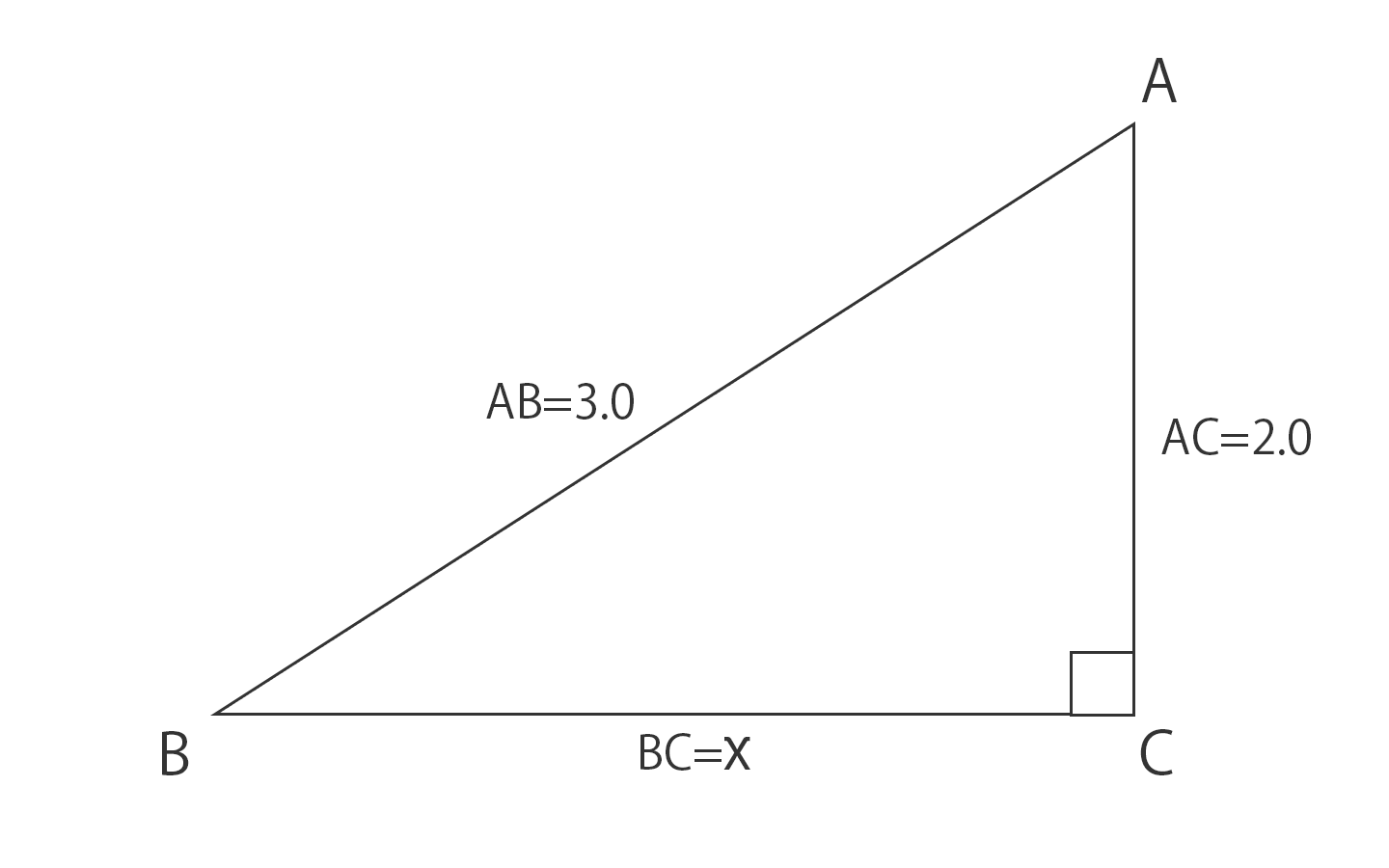
Python 三平方の定理 Unpyside

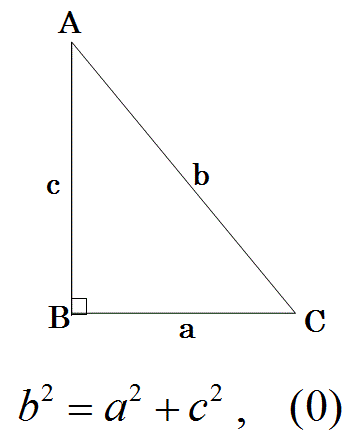
勉強しよう数学 拡張三平方の定理

三平方の定理で辺を求める Youtube

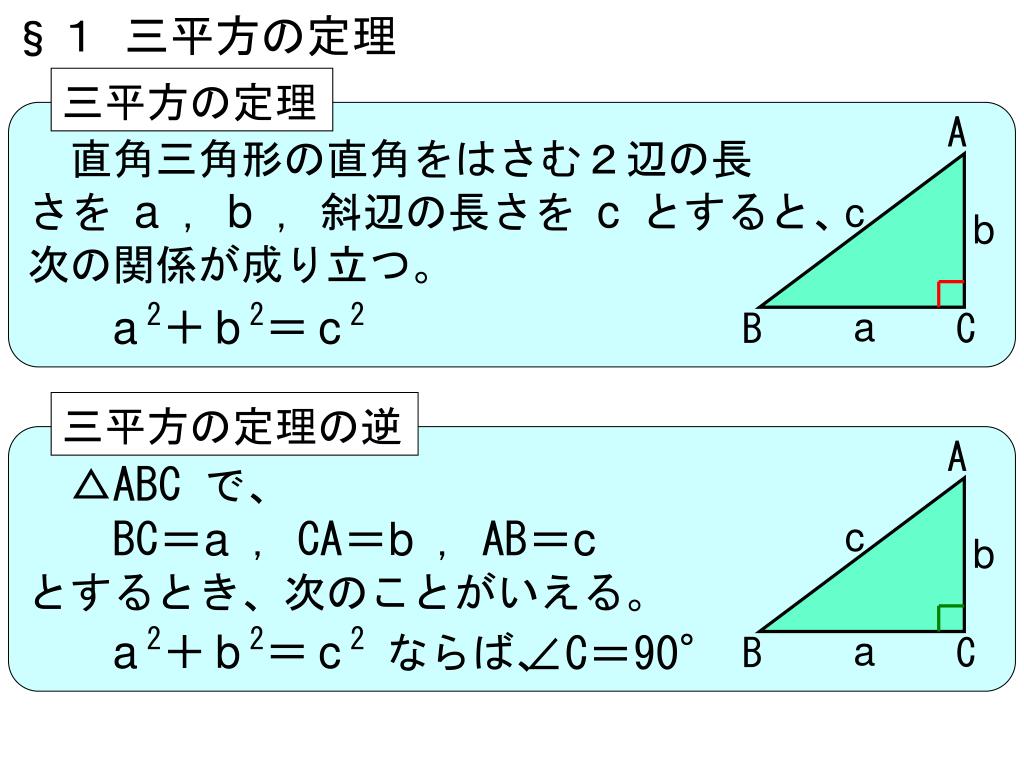
Ppt ６ 三平方の定理 Powerpoint Presentation Free Download Id

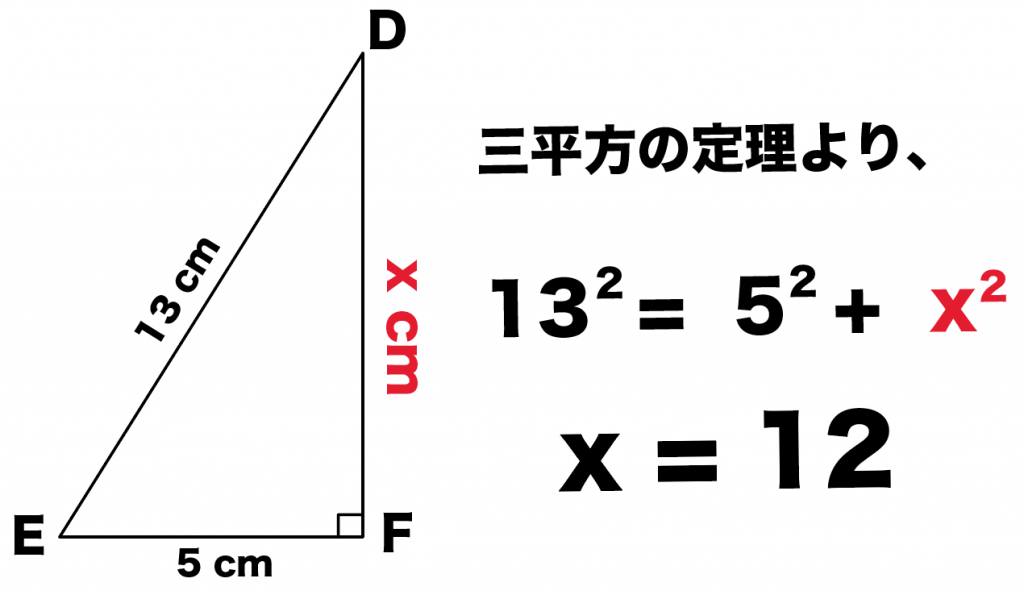
3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座

2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

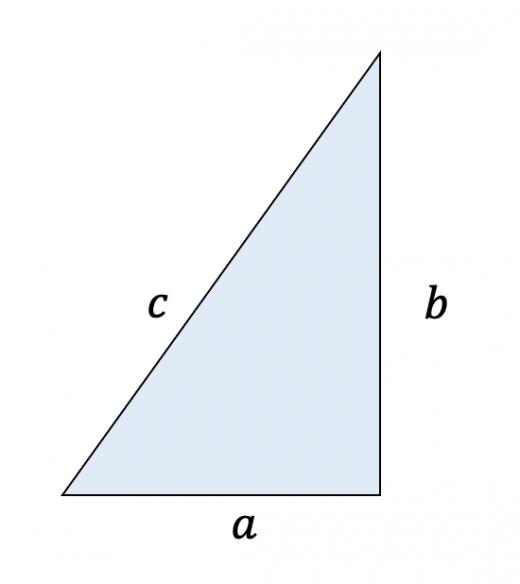
直角三角形の定義とさまざまな公式 高校数学の美しい物語

三平方の定理 やややさしい数学

1

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

三平方の定理 特別な直角三角形 イ弋マ本ゼミナール

3

数学 中3 61 三平方の定理 基本編 Youtube

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

直角三角形の辺の長さ 合同条件 面積について アタリマエ

โน ตของ 中学数学 三平方の定理のキホン ช น Junior Clearnote

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

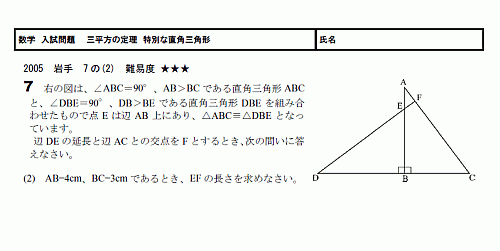
三平方の定理 スタディーx

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

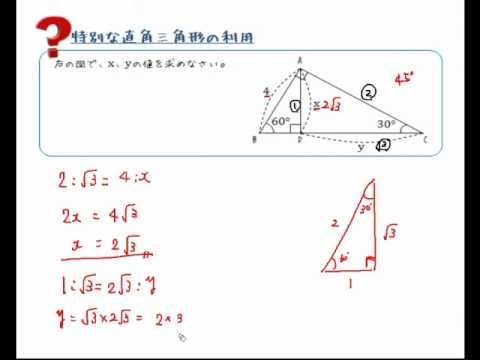
特別な直角三角形の利用 Youtube

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理の導入 Geogebra

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

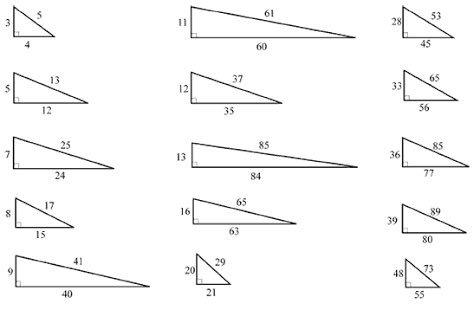
擔擔 予め覚えておくと便利な よく出る整数比になる直角三角形の例 別に知らなくても三平方の定理で出てくるわけだけど たとえば中上段の 11 2 60 2 3721だけど これが61の二乗であると知らなかったら 61が素数であることもあって が外せることに

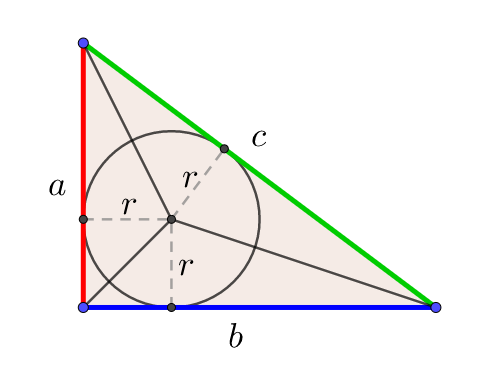
三平方の定理の証明４ 直角三角形と内接円 キソカラ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理の証明 直感的に分かる図で解説します 数学fun

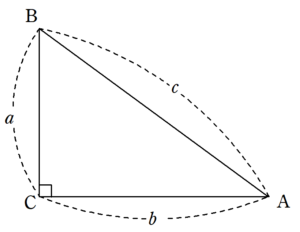
三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

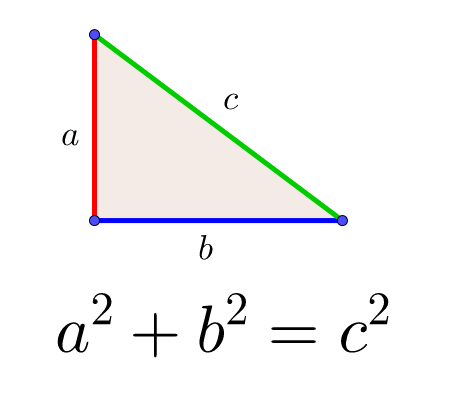
三平方の定理の証明２ ４つ直角三角形と真ん中の四角 キソカラ

三平方の定理の応用

Incoming Term: 三平方の定理 直角三角形だけ, 三平方の定理 直角三角形以外,